Ebben a kiadványban megvizsgáljuk, mi a Gauss-módszer, miért van rá szükség, és mi az elve. Gyakorlati példán keresztül bemutatjuk, hogyan alkalmazható a módszer lineáris egyenletrendszer megoldására.
A Gauss-módszer leírása
Gauss módszer megoldására használt változók szekvenciális eltávolításának klasszikus módszere. Nevét Carl Friedrich Gauss (1777-1885) német matematikusról kapta.
Először azonban emlékezzünk arra, hogy a SLAU képes:
- egyetlen megoldás;
- végtelen számú megoldásuk van;
- összeférhetetlen, azaz nincs megoldás.
Gyakorlati előnyök
A Gauss-módszer nagyszerű módja a háromnál több lineáris egyenletet tartalmazó SLAE megoldásának, valamint olyan rendszereknek, amelyek nem négyzet alakúak.
A Gauss-módszer elve
A módszer a következő lépéseket tartalmazza:
- egyenes – az egyenletrendszernek megfelelő kibővített mátrixot a sorok felett a felső háromszög (lépcsős) alakra redukáljuk, azaz a főátló alatt csak nullával egyenlő elemek legyenek.
- vissza – a kapott mátrixban a főátló feletti elemeket is nullára állítjuk (alsó háromszög nézet).
SLAE megoldási példa
Oldjuk meg az alábbi lineáris egyenletrendszert Gauss módszerrel.
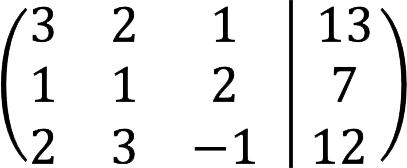
Megoldás
1. Először bemutatjuk az SLAE-t kiterjesztett mátrix formájában.
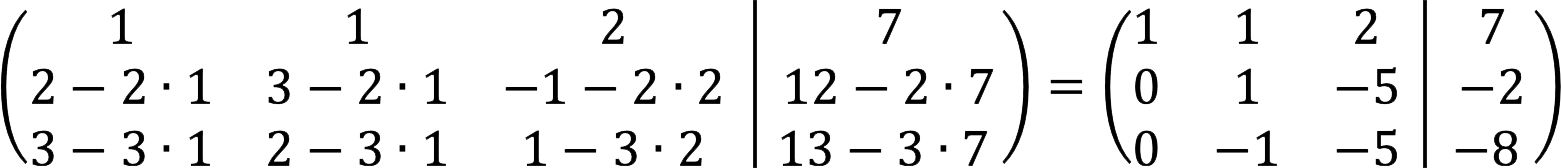
2. Most az a feladatunk, hogy a főátló alatti összes elemet visszaállítsuk. A további műveletek az adott mátrixtól függenek, az alábbiakban azokat ismertetjük, amelyek a mi esetünkre vonatkoznak. Először felcseréljük a sorokat, így az első elemeiket növekvő sorrendbe helyezzük.
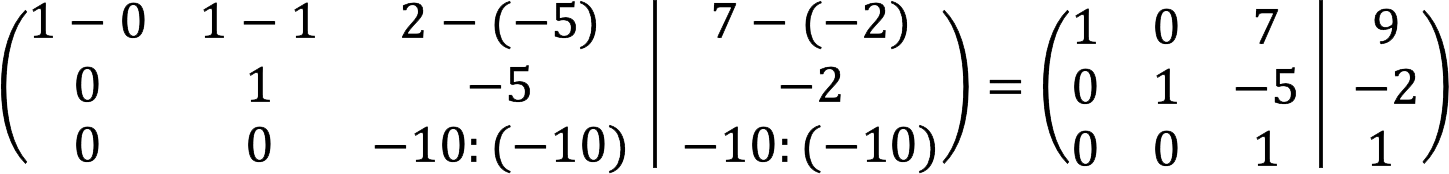
3. Vonja ki a második sorból kétszer az elsőt, a harmadikból pedig háromszorozza az elsőt.
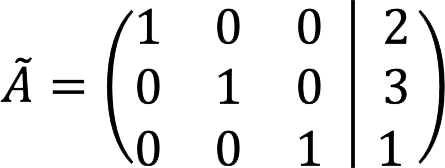
4. Adja hozzá a második sort a harmadikhoz.
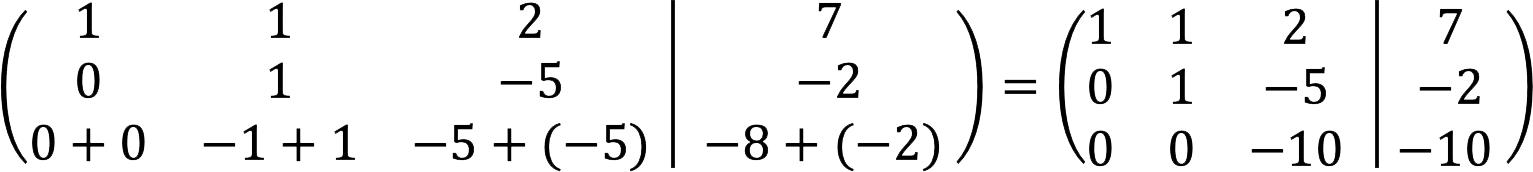
5. Vonja ki a második sort az első sorból, és ezzel egyidejűleg osszuk el a harmadik sort -10-zel.
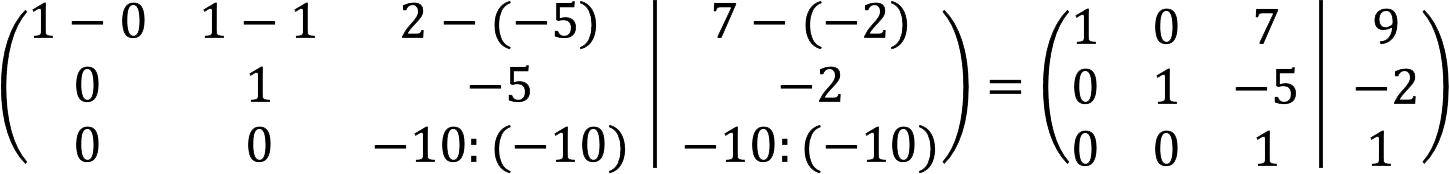
6. Az első szakasz befejeződött. Most meg kell kapnunk a null elemeket a főátló felett. Ehhez az első sorból vonjuk ki a harmadikat 7-tel szorozva, és adjuk hozzá a harmadikat 5-tel szorozva a másodikhoz.
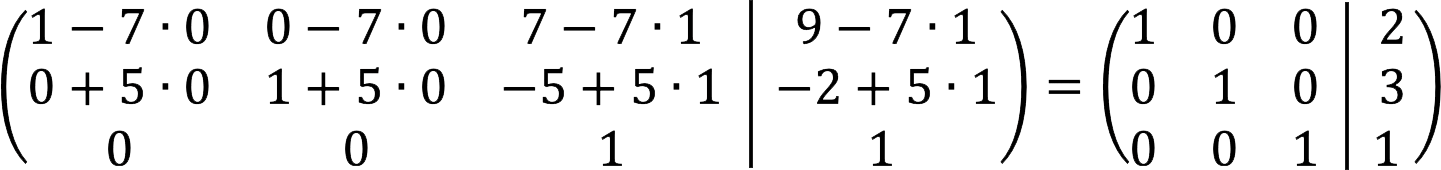
7. A végső kiterjesztett mátrix így néz ki:
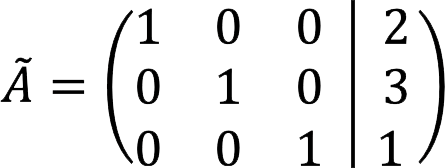
8. Megfelel az egyenletrendszernek:
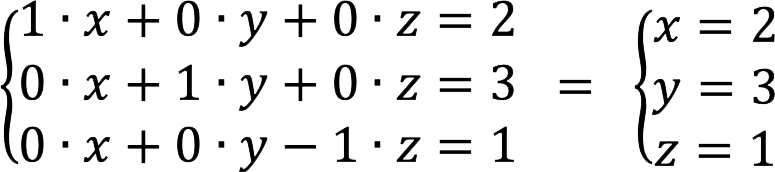
Válasz: gyökér SLAU: x = 2, y = 3, z = 1.










